Graph embeddings 2017 - Part I

Knowledge graphs

Introduction
Representation Learning
- Representation Learning in Vision & Text
- Representation learning in non-Euclidean domains
Graph embeddings
- Graph embeddings Challenges
- Applications of Graph embeddings
Conclusion

You can read the second part here if you want to jump into Graph embeddings right away.

Introduction

I have been working in the area of Network Representation Learning(aka. graph embeddings) for nearly a year now. Specifically, my work on graph embeddings deals with Knowledge graphs. So, I want to paint a high level picture about graph embeddings in general with this blog post. This blog post comprises of 2 sections - overview of representation learning, overview of graph embeddings. Which helps to build a foundation and big picture, before going in-depth in part-2.

Focus of this blog post

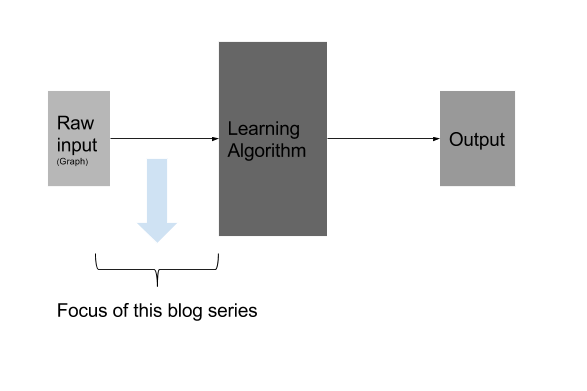
Focus of this blog post - input to algorithm

Moreover, I’m planning to write this as a 2-part series. That being said, subsequent part of the series will cover graph embeddings in depth. With the first part being this one, which you are currently reading right now. Second part will go in detail about the current research, state of art graph embedding techniques(approaches like random walk based , deep learning based, etc) in detail. The other subsequent parts I haven’t planned now would focus on the applied, code implementations side of graph embeddings, detailed write-up on the individual graph embeddings technique.

Machine learning - First Principles

Pedro Domingos, a CS professor at the University of Washington published a brief and immensely readable paper in 2012[1] that helpfully decomposed machine learning into three components: Representation, Evaluation, and Optimization. In this particular blog post, we are very much concerned about the representation part.

Machine learning three components

Many information processing tasks can be very easy or very diﬃcult depending on how the information is represented. This is a general principle applicable to daily life, to computer science in general, and to machine learning. For example, it is straightforward for a person to divide 210 by 6 using long division. The task becomes considerably less straightforward if it is instead posed using the Roman numeral representation of the numbers. Most modern people asked to divide CC by VI would begin by converting the numbers to the Arabic numeral representation, permitting long division procedures that make use of the place value system.[3]

Representation Learning

Representation is basically representing the input data(be image, speech, or video for that matter) in a way the learning algorithm can easily process. Representation Learning is using learning algorithms to derive good features or representation automatically, instead of traditional hand-engineered features. Specifically, during learning it transforms the raw data input to a representation that can be effectively exploited by learning algorithms. Hence this unsupervised feature learning obviates the need for manual feature engineering, which allows a machine to both learn the features and use them to perform a specific task.

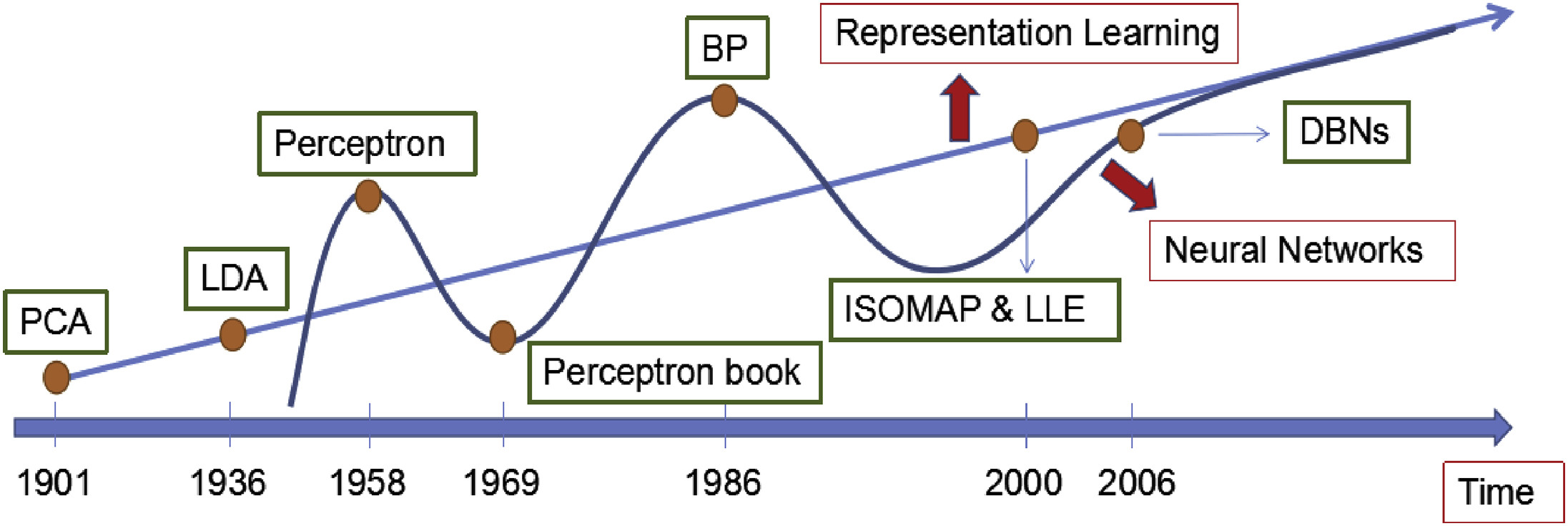
History and progress of Representation Learning

While looking back at older machine learning algorithms, they made great progress in training classification, regression and recognition systems when “good” representations, or features, of input data are available. They rely on the input being a feature and learn a classifier, regressor, etc on top of that. Most of these features were hand crafted, meaning, they were designed by humans. However, much human effort was spent on designing good features which are usually knowledge-based and engineered by domain experts over years of trial and error. A natural question to ask then is “Can we automate the learning of useful features from raw data?”. And the answer lied on representation learning(aka. feature engineering/learning).

representation learning history

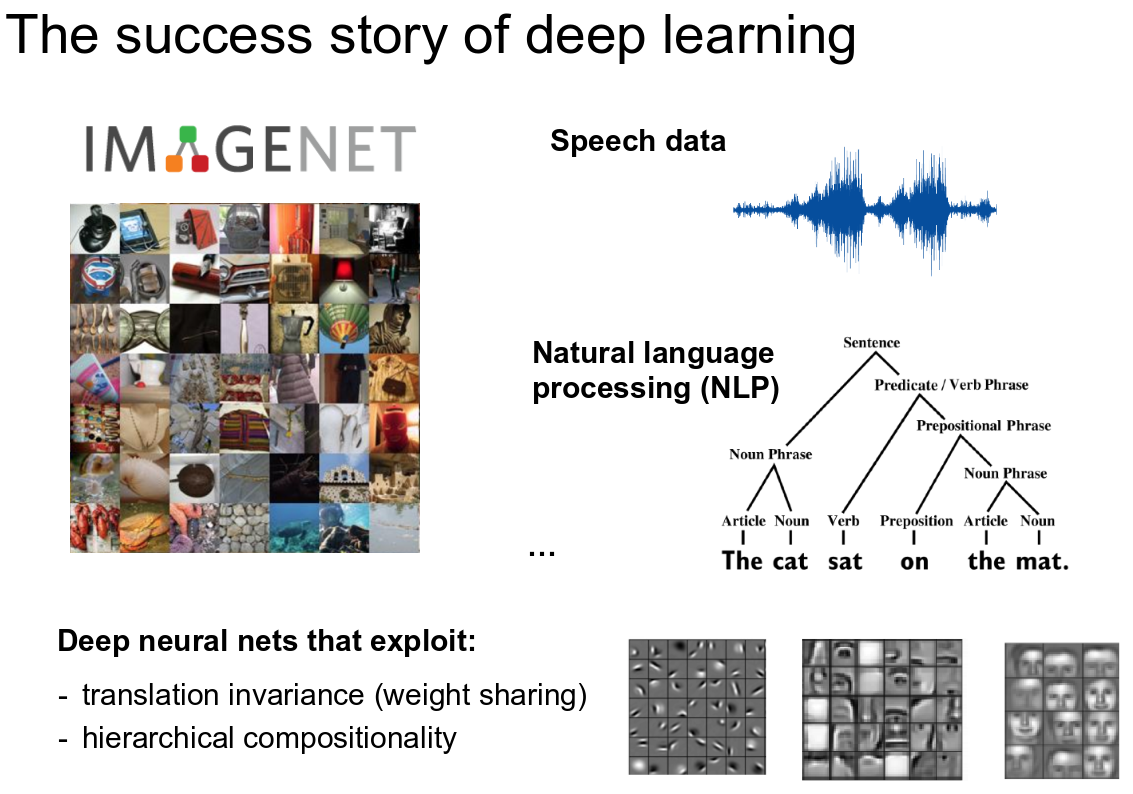
Representation Learning in Vision & Text

And coming to deep learning, it exploits this concept by its very nature. Multilayer neural networks can be used to perform feature learning, since they learn a representation of increasing complexity/abstraction of their input at the hidden layer(s) which is subsequently used for classification or regression at the output layer. While the representations or features learned corresponds to the hidden stochastic neurons. Specifically, Restricted Boltzmann machines, auto encoders, deep belief networks, convolutional neural networks are well known architectures for representation Learning. These learnt features are increasingly more informative through layers towards the machine learning task that we intend to perform (e.g. classification).

So basically, we have two learning tasks now. First, we let the deep network discover the features and next place our preferred learning model to perform your task. Simple!

Yoshua Bengio is one of the leaders in deep learning; although he began with a strong interest in the automatic feature learning that large neural networks are capable of achieving.

yoshua Bengio and representation learning

In his 2012 paper titled “Deep Learning of Representations for Unsupervised and Transfer Learning”[2] he commented:

“Deep learning algorithms seek to exploit the unknown structure in the input distribution in order to discover good representations, often at multiple levels, with higher-level learned features defined in terms of lower-level features”

Traits of representation learner

Furthermore, Deep models follow this modern view of representation learning[4] - learn representations (a.k.a. causes or features) that are

Hierarchical: representations at increasing levels of abstraction
Distributed: information is encoded by a multiplicity of causes
Shared among tasks
Sparse: enforcing neural selectivity
Characterized by simple dependencies: a simple (linear) combination of the representations should be sufficient to generate data

Success of deep learning

More often than not, how rich your input representation is has huge bearing on the quality of your downstream learning algorithms.

Representation Learning in NLP

Now let’s take a specific domain of natural language processing(NLP) and look at how representation learning and deep learning exploits this task.

If we look at the traditional legacy techniques of representing text(before deep learning) were one-hot encoding, Bag of words, N-gram, TF-IDF. Since these archaic techniques treat words as atomic symbols, every 2 words are equally apart. They don’t have any notion of either syntactic or semantic similarity between parts of language. This is one of the chief reasons for poor/mediocre performance of NLP based models. But this has changed dramatically in past few years.

one hot , bag of words

Representation of words as vectors(aka. embedding) is a very good example of representation learning. You could read about Word2Vec or GloVE where words are represented as vectors in a hyperspace. Due to its popularity, word2vec has become the de facto “Hello, world!” application of representation learning. When applying deep learning to natural language processing (NLP) tasks, the model must simultaneously learn several language concepts: the meanings of words, how words are combined to form concepts (i.e., syntax), how concepts relate to the task at hand. Word embeddings helps you achieve this -> king - man + woman = queen.

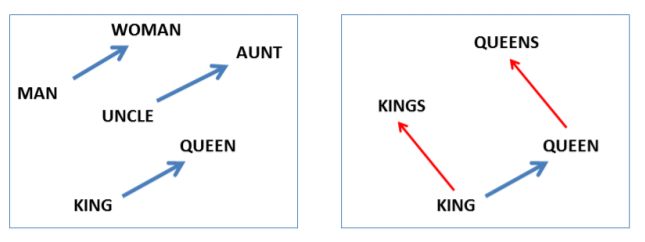
Word vector king queen

That is, when you perform this calculation over the vectors of king, man and woman, you would have a vector which would be very close to that of queen. This is what deep learning for word representation has helped to achieve.

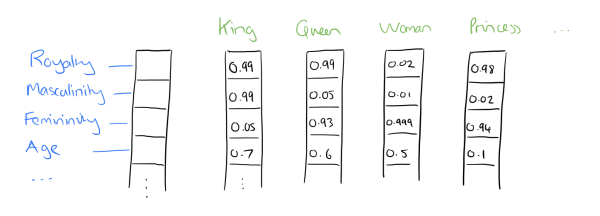
Embedding values for many words

Mathematically, embedding maps information entities into a dense, real-valued, and low-dimensional vectors. Specifically in NLP, it maps between space with one dimension per linguistic unit (character, morpheme, word, phrase, paragraph, sentence, document) to a continuous vector space with much lower dimension. Thus the “meaning” of linguistic unit is represented by a vector of real numbers.

Embedding example for a single word - man

Representation Learning in Computer vision

And in the field of computer vision; deep learning and representation learning provided state of art results for vision tasks like image classification, object detection,etc. Classical examples of features in computer vision include Harris, SIFT, LBP, etc. Images can be represented using these features and learning algorithms can be applied on top of that. We can have a neural network which takes the image as an input and outputs a vector, which is the feature representation of the image. This is the representation learner. This be followed by another neural network that acts as the classifier, regressor,etc.

Lets consider this example to make things clear. A wheel has a geometric shape, but its image may be complicated by shadows falling on the wheel, the sun glaring off the metal parts of the wheel, the fender of the car or an object in the foreground obscuring part of the wheel, and so on. One solution to this problem is to use ML to discover not only the mapping from representation to output but also the representation to itself. This approach is called representation learning.

Instead of manually describing the wheel; like, say it should be circular, be black in colour, have treads, etc. But these are all hand crafted features and may not generalize to all situations. For example, if you look at the wheel from a different angle, it might be oval in shape. Or the lighting may cause it to have lighter and darker patches. These kinds of variations are hard to account for manually. Instead, we can let the representation learning neural network learn them from data by giving it several positive and negative examples of a wheel and training it end to end.

That’s a wrap on the representation learning part. Let’s get deeper into Graph embeddings now (our topic of interest in this blog series).

Representation learning in non-Euclidean domains

In the last decade, deep learning techniques for representation learning disrupted the field of Computer Vision, speech and text, which we have seen above. That said, research on DL techniques has mainly focused so far on data defined on Euclidean domains (i.e. grids, sequences). There have been very few studies involving representation learning on network data (for example, social network data). Recently, methods which use the representation of graph nodes in vector space have gained traction from the research community.

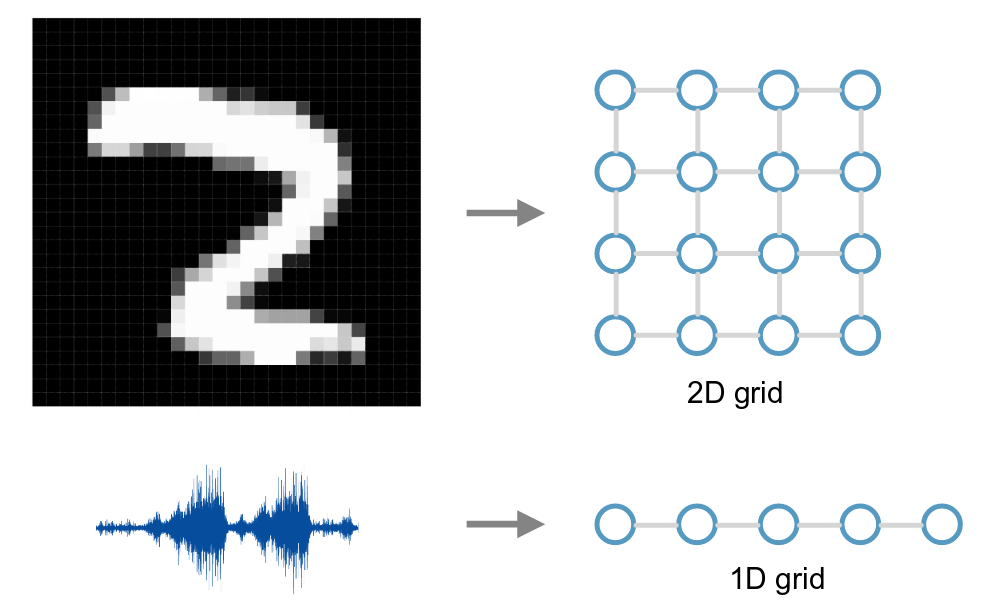
Eucledian data visualisation

Specifically, in a multitude of different fields, such as: Biology, Physics, Network Science, Recommender Systems and Computer Graphics; one may have to deal with data defined on non-Euclidean domains (i.e. graphs and manifolds). The adoption of Deep Learning in these particular fields has been lagging behind until very recently, primarily since the non-Euclidean nature of data makes the definition of basic operations (such as convolution) rather elusive. Geometric Deep Learning deals in this sense with the extension of Deep Learning techniques to graph/manifold structured data. Geometric Deep Learning is one of the most emerging fields of the Machine Learning community.

So, how can we represent non-euclidean data like graphs?

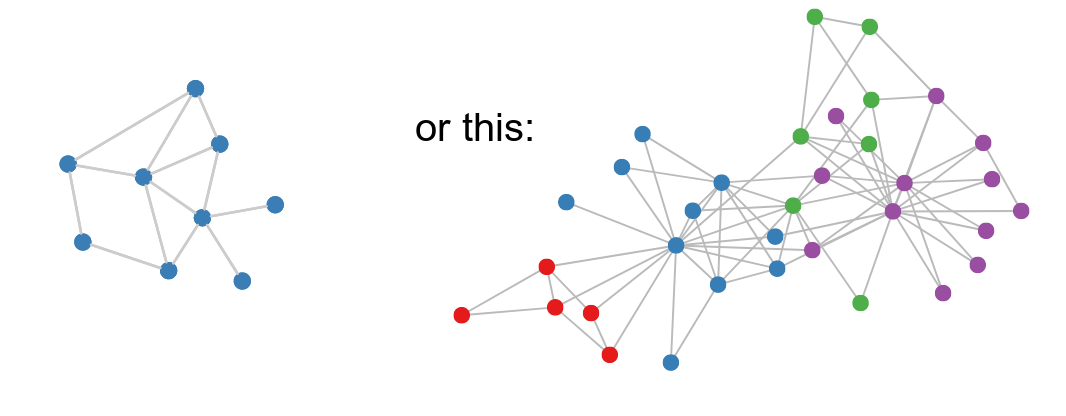
Graphs pictorial representation

Graphs are a ubiquitous data structure. Social networks, molecular graph structures, biological protein-protein networks, recommender systems—all of these domains and many more can be readily modeled as graphs, which capture interactions (i.e., edges) between individual units (i.e., nodes). As a consequence of their ubiquity, graphs are the backbone of countless systems, allowing relational knowledge about interacting entities to be efficiently stored and accessed. However, graphs are not only useful as structured knowledge repositories: they also play a key role in modern machine learning. The central problem in machine learning on graphs is finding a way to incorporate information about the structure of the graph into learning algorithms.

Traditionally, to extract structural information from graphs, traditional machine approaches often rely on summary graph statistics (e.g., degrees or clustering coefficients), kernel functions, or carefully engineered features to measure local neighborhood structures. However, these approaches are limited because these hand-engineered features are inflexible — i.e., they cannot adapt during the learning process and designing these features can be a time-consuming and expensive process.

Enter Graph embeddings

Generally, graph embedding aims to represent a graph as low dimensional vectors while the graph structure are preserved. We may represent a node or edge or path or substructure or whole-graph(at different levels of granularity) as a low-dimensional vector. And handle different kinds of networks (directed, weighted, temporal, multiplex, etc.). These learned embeddings are input as features to a model and the parameters are learned based on the training data. This obviates the need for complex classification models which are applied directly on the graph. The differences between different graph embedding algorithms lie in how they define the graph property to be preserved.

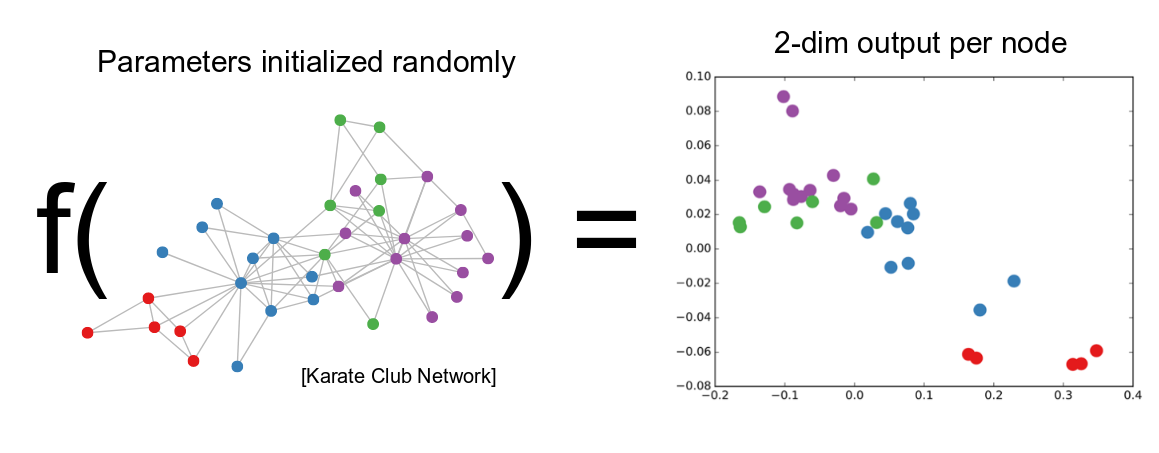
graph embedding visualisation

Moreover, the problem of graph embedding is related to two traditional research problems, i.e., graph analytics and representation learning. On the one hand, graph analytics aims to mine useful information from graph data. On the other hand, representation learning obtains data representations that make it easier to extract useful information when building classifiers or other predictors. Graph embedding lies in the overlapping of the two problems and focuses on learning the low-dimensional representations. Note that we distinguish graph representation learning and graph embedding here. Graph representation learning does not require the learned representations to be low dimensional.

Current methodology of dealing with large graph data is approached through Graph analytics. Effective graph analytics provides users a deeper understanding of what is behind the data, and thus can benefit a lot of useful applications such as node classification, node recommendation, link prediction, etc. However, most graph analytics methods suffer the high computation and space cost. While, graph embeddings converts the graph data into a low dimensional space in which the graph structural information and graph properties are maximally preserved.

Particularly, NLP and graph data work because graphs have a “natural affinity” with NLP, relation-oriented, providing index-free adjacency. While alleviating sparsity issue in large-scale NLP and enable knowledge transfer across domains and objects.

Graph embeddings Challenges

Embedding graphs into low dimensional space is not a trivial task. The challenges of graph embedding depend on the problem setting, which consists of embedding input and embedding output.

There are different types of graphs(e.g., homogeneous graph, heterogeneous graph, attribute graph, graph with auxiliary information, graph constructed from non-relational data, etc), so the input of graph embedding varies in different scenarios. Different types of embedding input carry different information to be preserved in the embedded space and thus pose different challenges to the problem of graph embedding. For example, when embedding a graph with structural information only, the connections between nodes are the target to preserve.

The output of graph embedding is a low-dimensional vector representing a part of the graph(or a whole graph). Unlike embedding input which is given and fixed, the embedding output is task driven. For example, the most common type of embedding output is node embedding which represents close nodes as similar vectors.

Node embedding can benefit the node related tasks such as node classification, node clustering, etc. However, in some cases, the tasks may be related to higher granularity of a graph e.g., node pairs, subgraph, whole graph. Hence the first challenge in terms of embedding output is how to find a suitable embedding output type for the specific application task.

We categorize four types of graph embedding output, including node embedding, edge embedding, hybrid embedding and whole-graph embedding. Different output granularities have different criteria of what a ”good” embedding and face different challenges. For example, a good node embedding preserves the similarity to its neighbour nodes in the embedded space. In contrast, a good whole-graph embedding represents a whole graph as a vector so that the graph-level similarity is preserved.

Furthermore, Choice of property, Scalability, Dimensionality of the embedding are other few challenges that has to be addressed.

Choice of property : A “good” vector representation of nodes should preserve the structure of the graph and the connection between individual nodes. The first challenge is choosing the property of the graph which the embedding should preserve. Given the plethora of distance metrics and properties defined for graphs, this choice can be difficult and the performance may depend on the application.
Scalability : Most real networks are large and contain millions of nodes and edges — embedding methods should be scalable and able to process large graphs. Defining a scalable model can be challenging especially when the model is aimed to preserve global properties of the network.
Dimensionality of the embedding: Finding the optimal dimensions of the representation can be hard. For example, higher number of dimensions may increase the reconstruction precision but will have high time and space complexity. The choice can also be application-specific depending on the approach: E.g., lower number of dimensions may result in better link prediction accuracy if the chosen model only captures local connections between nodes.

Applications of Graph embeddings

Having said all the above. You might ask; where will I make use of Graph embeddings. Graph embedding has been adopted in many different applications as the vector representations can be processed efficiently in both time and space. The applications fall under three of three following categories: node related, edge related and graph related.

Node Related Applications - Node Classification and semi-supervised learning, Clustering, Node Recommendation/Retrieval/Ranking, Clustering and community detection.
Edge Related Applications - Link Prediction and Graph Reconstruction.
Graph Related Application - Graph Classification, Visualization and pattern discovery, Network compression.

Conclusion

This post was meant to provide a the fundementals required for graph embeddings. Please let me know your feedback in the comments below.

Thanks for reading. Cheers!

We’ve come to the end of the first part of the blog series. You can check the second part here. Which will provide a big-picture for learning and getting started with graph embeddings.